rkock guitars & amps

Elektrotechnische Grundlagen

Allgemeines

Damit man die Berechnungen der Röhren-Verstärker auf den folgenden Seiten versteht, sollen hier ein paar grundlegende Gesetze und Formeln für die elektrischen Stromkreise aufgeführt werden. Diese Erklärungen sind möglichst einfach gehalten. Wer es physikalisch und mathematisch genau hergeleitet haben will, sollte in die entsprechenden Fachbücher der E-Technik schauen.

Die Gleichstromtechnik

Das Ohmsche Gesetz

Dies Gesetz besagt, dass in einem (linearen) elektrischen Stromkreis mit der Spannungsquelle U der Strom I proportional zur Spannung ist:

U ^~ I .

Berücksichtigt man noch den Widerstand als Proportionalitätsfaktor, so ergibt sich daraus:

Diese Formel kann man jetzt auch umstellen:

Dies besagt dann, dass der Strom im Stromkreis umgekehrt proprotional dem Widerstand ist:

^{I ~ 1 / R .}

^{Mit anderen Worten ausgedrückt, je höher in einem elektrischen Stromkreis der Widerstand ist, desto kleiner wird der Strom (bei konstanter Spannung).}

^{Hier noch die Einheiten:}

• ^{Spannung U: Volt [V]}
• ^{Strom I: Ampere [A]}
• ^{Widerstand R: [V/A]}

Dies Ohmsche Gesetz gilt für Gleichstromtechnik, hat aber in der Wechselstromtechnik grundsätzlich die gleiche Gültigkeit.

^{Die elektrischen  Leistung}

Die in einem elektrischen Stromkreis einem Widerstand zugeführte Leistung P berechnet sich aus dem Produkt von Spannung und Strom:

Die Leistung hat die Einheit  Watt [W] = [VA].

Man kann dies jetzt noch anders ausdrücken, indem man das Ohmsche Gesetz anwendet und die Gleichung 2 einsetzt:

P = U x I  ->

oder die Gleichung 1 einsetzt:

Die Kirchhoff'schen Gesetze

Eine elektrische Schaltung besteht in der Praxis grundsätzlich aus mehreren Widerständen und u.U. auch aus mehreren Spannungsquellen. Dann wird solch eine Schaltung auch elektrisches Netzwerk genannt. Für die Berechnung in einem elektrischen Netzwerk gibt es zwei wichtige Regeln, nämlich die zwei Kirchhoff'schen Gesetze.

Das erste Kirchhoff'sche Gesetz besagt, dass in einem Netzwerk, in dem sich mehrere Knotenpunkte befinden, die Summe der zufließenden Ströme gleich der Summe der abfließenden Ströme ist:

Angewendet auf obiges Netzwerk bedeutet dies, dass der auf den Knotenpunkt (A) zufließende Strom I₁ gleich der Summe der abfließenden Ströme I₂ + I₃ ist.
Dieses Gesetz wird als Knotengleichung bezeichnet.

Das zweite Kirchhoff'sche Gesetz bezieht sich auf Maschen in einem Netzwerk. Als Maschen bezeichnet man in einer Schaltung auftretende geschlossene Wege (z.B. in folgendem Bild die Maschen I oder II).

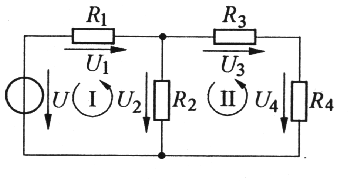
Das Gesetz besagt, dass die Summe der in einer Masche auftretenden Spannung immer gleich Null ist:

Für obiges Netzwerk bedeutet dies: Es lassen sich zwei Gleichungen aufstellen:

Masche I: U - U₁ - U₂ = 0
Masche II: U₂ - U₃ - U₄ = 0

Mit Hilfe dieser Gleichungssysteme lassen sich dann die Ströme, Spannungen etc. berechnen.
Dies Gesetz wird als Maschengleichung bezeichnet.

Reihenschaltung von Widerständen

Werden Widerstände hintereinander geschaltet, so bezeichnet man das als Reihenschaltung (von Widerständen).

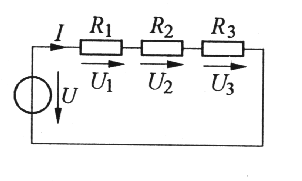
Der Gesamtwiderstand dieser Reihenschaltung berechnet sich nach dem Ohmschen Gesetz und der Tatsache, dass durch alle Widerstände der gleiche Strom I fließt zu:

Es gilt weiterhin für eine Reihenschaltung von Widerständen, dass sich die Teilspannungen (U₁, U₂, etc. an den Widerständen) verhalten wie die Teilwiderstände.

Dies rührt daher, dass alle Widerstände in einer Reihenschaltung vom gleichen Strom durchflossen werden.
Dies bezeichnet man auch als Spannungsteilerregel.

Ein typischer Anwendungsfall für einen Spannungsteiler ist das folgende Bild.

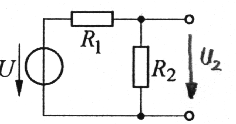
Zu berechnen ist dabei die Spannung U2 am Widerstand R2.
Entsprechend der Spannungsteilerregel (Gl. 9) gilt für obiges Netzwerk:

U₂/U = R₂/(R₁ + R₂)   --> 

Parallelschaltung von Widerständen

Bei der Parallelschaltung von Widerständen liegt an allen Widerständen (R1, R2, R3) die gleiche Spannung.

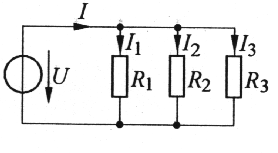
Für den Gesamtwiderstand gilt unter Berücksichtigung des Ohmschen Gesetzes und des ersten Kirchhoff'schen Gesetzes (Gl. 6) folgende Formel für den Gesamtwiderstand:

Da eine Parallelschaltung oft nur aus zwei Widerständen besteht, hier noch die Formel für die Parallelschaltung von zwei Widerständen:

Unter Berücksichtigung des Ohmschen Gesetzes gilt folgendes Gesetz:

Dies bedeutet, dass sich die Teilströme umgekehrt wie die Widerstände verhalten.
Dieses Gesetz nennt man die Stromteiler-Regel.

Ideale Spannungsquelle mit Innenwiderstand

Jede reale Spannungsquelle kann man sich vorstellen als ideale Spannungsquelle U_q mit nachgeschalteten Innenwiderstand R_i.

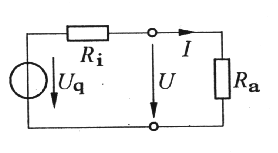
Wird solch eine Spannungsquelle nicht mit einem Widerstand belastet (der Belastungswiderstand ist unendlich hoch), so ergibt sich an den beiden äußeren Klemmen dieser realen Spannungsquelle eine Spannung U, die gleich dem Wert der Quellenspannung U_q ist.

Dies ergibt sich aus der Tatsache, dass der Stromkreis nicht geschlossen ist und damit am Innenwiderstand R_i keine Spannung abfällt. An den beiden Klemmen steht die Leerlaufspannung U an.

Wird die Spannungsquelle dagegen mit einem Widerstand R_a belastet, so ergibt sich die Klemmenspannung zu

U = U_q - (I x R_i)        mit  I = U_q / (R_i + R_a) .        

Wird an den äußeren Klemmen parallel zum Widerstand ein Draht mit 0 Ohm Widerstand angeschlossen, so handelt es sich um einen Kurzschluß. Damit spielt dieser Widerstand keine Rolle mehr, da der ganze Strom den Weg über den Kurzschluß nimmt. An den Klemmen kann keine Spannung mehr gemessen werden.
In obiger Gleichung wird die Spannung U = 0. Daraus ergibt sich

0 = U_q - (I x R_i) . Stellt man diese Gleichung so um, dass man daraus den Strom ermitteln kann, so ergibt sich der Strom I_k zu:

Dies ist der Kurzschlußstrom dieser realen Spannungsquelle.

Leistungsanpassung

Für viele Verstärkerschaltungen (z.B. Röhrenendstufe) ist es wichtig, dass an einen Lautsprecher (Widerstand) die maximale Leistung abgegeben wird.

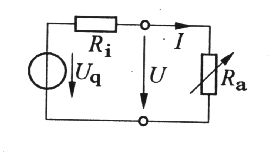
Wird eine reale Spannungsquelle, die sich aus der Quellenspannung  und dem Innenwiderstand  ergibt, mit einem äußeren Widerstand belastet, so gilt für die Leistung an R_a:

P_a = U x I .

I = U_q / (R_i + R_a)

U = I R_a = R_a x U_q / (R_i + R_a) .

Die dem Widerstand zugeführte Leistung ist dann

Macht man den Widerstand variabel, so kann man zwei Extremwerte betrachten:

R_a=0: P_a=0 (keine Spannung am Widerstand R_a)

R_a=Unendlich: P_a=0, (kein Strom durch den Widerstand R_a).

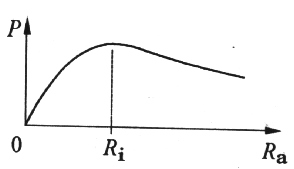
Anwendung mathematischer Methoden auf die obige Leistungs-Formel (15) ergibt, dass die max. Leistung dann an den Widerstand R_a abgegeben wird, wenn gilt:

Dies bedeutet also, dass der Lautsprecher-Widerstand gleich dem Innenwiderstand des Endverstärkers sein muß, soll eine optimale Leistungsabgabe an den Lautsprecher erfolgen.
Betrachtet man obiges Bild, so wird der R_a-Bereich zwischen 0 und  R_i als Unteranpassung bezeichnet, der Bereich rechts von R_i als Überanpassung.
Im Bereich der Unteranpassung ergeben sich sehr schnell hohe Ströme und man nähert sich dem Kurzschlußstrom. Für stromverstärkende Transistor-Endverstärker gefährlich, sofern sie keine Kurzschluß-Sicherung haben.
Im Bereich der Überanpassung nähert man sich erst mit hohen Werten von R_a der Leerlaufspannung. Für spannungsverstärkende Endverstäker wie Röhren-Endstufen gefährlich. Dazu später mehr.

[Inhalt] [zurück] [weiter]
Copyright © 1999/2016 by rkock guitars & amps
Zuletzt geändert am: 25. Februar 2016